Estimation of exchange interactions

Author: Takuya Nomoto

Liechtenstein method

The Liechtenstein method is a method for deriving the classical spin models from the itinerant electron models. Initially developed by Liechtenstein et al.[1] in the framework of the spin density functional theory, the method has been applied to various systems and is successful in understanding many magnetic behaviors, including finite temperature effects and long-period magnetic structures, which are not accessible from the spin density functional theory alone. Here, as the simplest case, we will see the formulation for the single-orbital model, where we can use the sparse_ir library to accelerate the calculations.

Liechtenstein formula in single-orbital model

Let us consider to derive exchange interactions from the following one-body Hamiltonian:

\[ \begin{align} H=-t\sum_{<i,j>}\sum_s c^\dagger_{is} c_{js} - \sum_i \sum_{ss'} c^\dagger_{is} (\boldsymbol{B_i} \cdot \boldsymbol{\sigma}_{ss'}) c_{is'} \end{align} \]

If we set the effective magnetic field \(\boldsymbol{B}_i\) to \(\boldsymbol{B}_i=JS\boldsymbol{e}_i/2\), this is a classical Kondo lattice model, while if \(\boldsymbol{B}_i=U\boldsymbol{m}_i/2\), this is a Hubbard model with the mean-field approximation. The basic idea of the Liechtenstein method is to impose the equivalence of the spin-angle-derivatives of the total energies in the itinerant systems and the classical spin systems. Note that the derivatives generally depend on a reference magnetic structure. Here, let us consider the classical Heisenberg model \(E=-2\sum_{<i,j>}J_{ij}\boldsymbol{e}_i\cdot \boldsymbol{e}_j\) as a spin model and the \(\hat{z}\)-polarized ferromagnetic state (namely, \(\boldsymbol{B_i}=B\hat{z}\)) as a reference magnetic structure. Then, we will get

\[ \begin{align} J_{ij} = -B^2T\sum_{\omega_n} G_{ij,+}(i\omega_n)G_{ji ,-}(i\omega_n) \end{align} \]

where the Green function \(G_{ij,\sigma}(i\omega_n)\) is a Fourier transform of \(G_{\boldsymbol{k},\sigma}(i\omega_n) = [i\omega_n - (\varepsilon_{\boldsymbol{k}}-B\sigma-\mu)]^{-1}\) with the single-particle dispersion \(\varepsilon_{\boldsymbol{k}}\) and chemical potential \(\mu\). \(i\omega_n=(2n+1)\pi T\) is the Matsubara frequency and \(\boldsymbol{k}\) is the crystal momentum. An important quantity here is defined by \(J_0=\sum_{0\neq i}J_{0i}\), which is related to the mean-filed transition temperature \(T_c^{\rm mf}\) in the classical Heisenberg model by \(T_c^{\rm mf}=2J_0/3\). This can be evaluated from the above \(J_{ij}\), or the direct comparison of the second derivatives of the total energy, which gives

\[ \begin{align} J_0 = \frac{B}{2} (n_{0,+}- n_{0,-})+ B^2T\sum_{\omega_n} G_{00,+}(i\omega_n)G_{00,-}(i\omega_n) \end{align} \]

In practice, \(G_{00,\sigma}(i\omega_n)\) can be obtained by the \(\boldsymbol{k}\) summation of \(G_{\boldsymbol{k},\sigma}(i\omega_n)\) since all sites are equivalent in this model. Thus, the number of operations is \(\mathcal{O}(N_M N_k^{tot})\) where \(N_M\) is the number of Matsubara frequency and \(N_k^{tot}\) is the total number of k-points. Since the typical value of \(N_M\) is \(N_M\sim \beta W\), the total cost is given by \(\mathcal{O}(\beta W N_k)\). On the other hand, we need \(G_{ij,+}(i\omega_n)\) to evaluate \(J_{ij}\), and in this case, the number of operations becomes \(\mathcal{O}(N_M (N_k\ln N_k)^d)\) since the Fourier transform requires \(N_k\ln N_k\) operations for a single axis, where \(N_k\) is the number of k-points for a single axis and \(d\) is the dimension. Thus, we need \(\mathcal{O}(\beta W (N_k\ln N_k)^d)\) in total.

Sparse_ir

Since \(G_{ij,\sigma}(i\omega_n)\) as well as \(G_{00,\sigma}(i\omega_n)\) are just linear conbinations of \(G_{\boldsymbol{k},\sigma}(i\omega_n)\), all terms we need take the following form,

\[ \begin{align} \frac{1}{i\omega_n - \varepsilon_a}\frac{1}{i\omega_n - \varepsilon_b}=\frac{1}{\varepsilon_a-\varepsilon_b}\left(\frac{1}{i\omega_n - \varepsilon_a}-\frac{1}{i\omega_n - \varepsilon_b} \right) \end{align} \]

Thus, we can expand \(G_{ij,+}(i\omega_n)G_{ji ,-}(i\omega_n)\) in the expression for \(J_{ij}\) and \(G_{00,+}(i\omega_n)G_{00,-}(i\omega_n)\) for \(J_{0}\) by the intermadiate representation. Since the summation over \(i\omega_n\) is equivalent to evaluating the Fourier transform at \(\tau=0\), we need only \(\mathcal{O}(\ln (\beta W))\) operations for the Matsubara frequancy axis. Thus, the computational cost becomes \(\mathcal{O}(\ln(\beta W) N_k^{tot})\) for \(J_0\) and \(\mathcal{O}(\ln(\beta W) (N_k\ln N_k)^d)\) for \(J_{ij}\).

Code implementation

Here, let us see an example code in a square lattice tight-binding model with dispersion \(\varepsilon_{\boldsymbol{k}} = -2t\,[\cos(k_x) + \cos(k_y)]\). First, we load all necessary modules that we need:

import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import sparse_ir

Parameter setting

The parameters to define the system are as follows; \(t\): the nearest-neighbor hopping amplitude, \(\beta\): the inverse temperature, \(N_k\): the numer of k-poitns for a single-axis and \(B\): the strengh of the effective magnetic field.

t = 1 # means the bandwidth W is W=8t in a square lattice model
beta = 50 # inverse temperature
nk = 36 # number of k-points for a signle-axis
b_eff = 3 # strength of the effective magnetic field

Liechtenstein solver

This class contains two solvers, j0_calc for calculation of \(J_{0}\) and jij_calc for \(J_{ij}\). Both can be called after instantiating the class.

class liechtenstein:
  def __init__(self, basis, *args):
    # constructor of liechtenstein class
    # the class requires five arguments: sparse_ir basis object, t, beta, nk, and b_eff
    
    self.basis, self.M, self.T = basis, sparse_ir.MatsubaraSampling(basis), sparse_ir.TauSampling(basis)
    t, self.beta, self.nk, self.b_eff= args[0], args[1], args[2], args[3]
    k1, k2 = np.meshgrid(np.arange(self.nk)/self.nk, np.arange(self.nk)/self.nk, indexing='ij')
    self.ek = -2* t * (np.cos(2*np.pi*k1) + np.cos(2*np.pi*k2))
    self.nkt = self.nk**2

  def j0_calc(self, e_range=np.zeros(1), NM=None):
    # solver to evaluate J_0
    # e_range: numpy ndarray object to specify the chemical potentials at which we evaluate J_0
    # NM: maximum number of Matsubara frequency. if None, sparse sampling will be used
  
    # set Matsubara frequency grid
    if NM is None: iw = 1j*np.pi*self.M.sampling_points/self.beta
    else         : iw = 1j*np.pi*(2*np.arange(-NM,NM)+1)/self.beta

    # calculate the first term in the expresson of J_0
    n_up = .5 * (1-np.tanh(.5*self.beta*(self.ek[None,:,:]-e_range[:,None,None]-self.b_eff)))
    n_dn = .5 * (1-np.tanh(.5*self.beta*(self.ek[None,:,:]-e_range[:,None,None]+self.b_eff)))
    j0_1 = .5 * self.b_eff * np.mean(n_up - n_dn, axis=(1,2))
        
    # calculate the second term in the expression of J_0 as a function of iw 
    gkio_up = 1/(iw[:,None,None,None] - (self.ek[None,None,:,:]-self.b_eff-e_range[None,:,None,None]))
    gkio_dn = 1/(iw[:,None,None,None] - (self.ek[None,None,:,:]+self.b_eff-e_range[None,:,None,None]))
    gio_up = np.mean(gkio_up, axis=(2,3))
    gio_dn = np.mean(gkio_dn, axis=(2,3))
    j0_2_w = self.b_eff**2 * gio_up * gio_dn
    
    # evaluate a summation over iw 
    if NM is None:
      j0_2_l = self.M.fit(j0_2_w.reshape(len(iw),len(e_range))) # transform to the intermediate representation
      j0_2 = self.basis.u(0)@j0_2_l # evaluate the function at \tau=0
    else:
      j0_2 = np.sum(j0_2_w,axis=0)/self.beta
    
    # sum up the two terms
    self.j0 = np.real(j0_1 + j0_2)
    self.j0_e_range = e_range

  def jij_calc(self, mu=0, NM=None):
    # solver to evaluate J_ij
    # mu: the chemical potential at which we evaluate J_ij
    # NM: maximum number of Matsubara frequency. if None, sparse sampling will be used
    
    # set Matsubara frequency grid
    if NM is None: iw = 1j*np.pi*self.M.sampling_points/self.beta
    else         : iw = 1j*np.pi*(2*np.arange(-NM,NM)+1)/self.beta
        
    # calculate J_ij as a function of iw 
    gkio_up = 1/(iw[:,None,None] - (self.ek[None,:,:]-self.b_eff-mu))
    gkio_dn = 1/(iw[:,None,None] - (self.ek[None,:,:]+self.b_eff-mu))
    grio_up = np.fft.fftn(gkio_up,axes=(1,2))/self.nkt
    grio_dn = np.fft.ifftn(gkio_dn,axes=(1,2))
    jij_w = - self.b_eff**2 * grio_up * grio_dn
    
    # evaluate a summation of J_ij over iw 
    if NM is None:
      jij_l = self.M.fit(jij_w.reshape(len(iw),self.nkt))
      jij = self.basis.u(0)@jij_l
    else:
      jij = np.sum(jij_w,axis=0)/self.beta
    
    # arrange the format to ouput the data
    self.jij = np.real(jij)
    self.jij[0] = 0
    self.jij_r = np.linalg.norm(np.array(np.meshgrid(np.arange(self.nk),np.arange(self.nk), indexing='ij')), axis=0).flatten()

Instantiation

In the instantation, we have to pass a sparse_ir.basis object as the first argument of the liechtenstein class.

Lambda = 2*max(8*t, b_eff) * beta
basis = sparse_ir.FiniteTempBasis(statistics='F', beta=beta, wmax=Lambda, eps=1e-7)
l = liechtenstein(basis, t, beta, nk, b_eff)

Executing the solver for J_0

Here, let us evaluate J_0 as a function of the chemmical potential \(\mu\). To check the validity of the sparse sampleing method, we will compare it with that evaluated by the conventional Matsubara frequency grid. This can be done as follows:

plt.xlabel("mu")
plt.ylabel("J_0")
for i, nm in enumerate([100, 200, 400, 800, 1600]):
      l.j0_calc(e_range=np.linspace(-10,10,41), NM=nm)
      plt.plot(l.j0_e_range, l.j0, marker='.', label=str(nm), color=cm.cool(i/5.))
l.j0_calc(e_range=np.linspace(-10,10,41))
plt.plot(l.j0_e_range, l.j0, marker='.', label='Sparse_IR', color=cm.cool(1.0))
plt.legend()
plt.show()

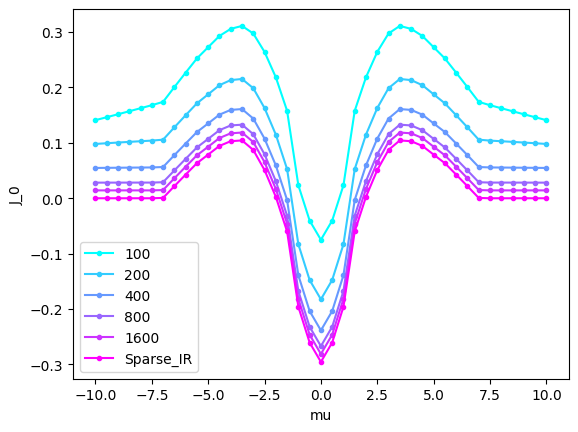
As is expected, the system favors the antiferromagnetic state at the half-filling while it favors the ferromagnetic state at the low-carrier regime. This feature is consistent with the super-exchange and the doule-exchange interactions.

Executing the solver for J_ij

We can also evaluate J_ij by using jij_calc function as follows.

plt.clf
plt.xlabel("distance")
plt.ylabel("J_ij")
plt.xlim([0,5])
l.jij_calc(0)
plt.scatter(l.jij_r, l.jij, marker='.')
plt.show()

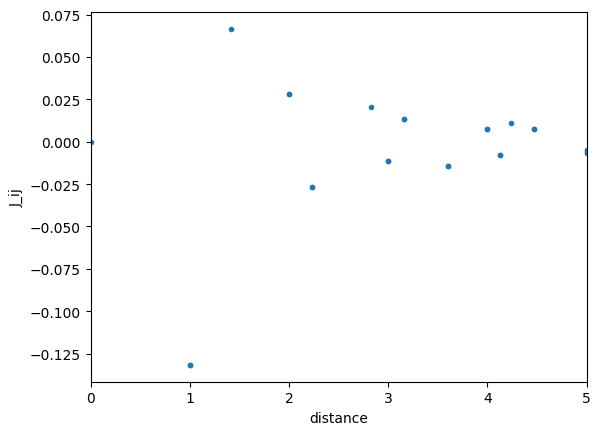
We can easily check \(J_0=\sum_j J_{0j}\) as follows.

J0_1 = l.j0[20]   # J0 at mu=0 evaluated by j0_calc
J0_2 = sum(l.jij)  
print(J0_1,J0_2)

-0.2954591400058828 -0.2954591398013725

[1] Liechtenstein et al., J. Phys. F: Met. Phys. 14 L125 (1984).