Transformation from/to IR

\[ \newcommand{\iv}{{\mathrm{i}\nu}} \newcommand{\wmax}{{\omega_\mathrm{max}}} \newcommand{\dd}{{\mathrm{d}}} \]

In this section, we explain how to transform numerical data to IR.

Poles

We consider a Green’s function genereated by poles:

\[ G(\iv) = \sum_{p=1}^{N_\mathrm{P}} \frac{c_p}{\iv - \omega_p}, \]

where \(\nu\) is a fermionic or bosonic Matsubara frequency. The corresponding specral function \(A(\omega)\) is given by

\[ A(\omega) = \sum_{p=1}^{N_\mathrm{P}} c_p \delta(\omega - \omega_p). \]

The modified (regularized) spectral function reads

\[\begin{split} \rho(\omega) = \begin{cases} \sum_{p=1}^{N_\mathrm{P}} c_p \delta(\omega - \omega_p) & \mathrm{(fermion)},\\ \sum_{p=1}^{N_\mathrm{P}} (c_p/\tanh(\beta \omega_p/2)) \delta(\omega - \omega_p) & \mathrm{(boson)}. \end{cases} \end{split}\]

for the logistic kernel. We immediately obtain

\[\begin{split} \rho_l = \begin{cases} \sum_{p=1}^{N_\mathrm{P}} c_p V_l(\omega_p) & \mathrm{(fermion)},\\ \sum_{p=1}^{N_\mathrm{P}} c_p V_l(\omega_p)/\tanh(\beta \omega_p/2))& \mathrm{(boson)}. \end{cases} \end{split}\]

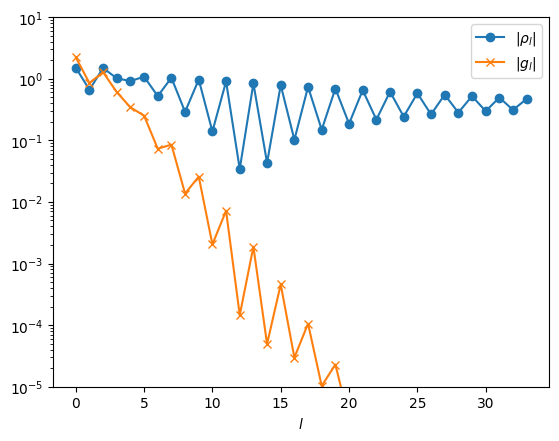
The following code demostrates this transformation for bosons.

import sparse_ir
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt

beta = 15
wmax = 10
basis_b = sparse_ir.FiniteTempBasis("B", beta, wmax, eps=1e-10)

coeff = np.array([1])
omega_p = np.array([0.1])

rhol_pole = np.einsum('lp,p->l', basis_b.v(omega_p), coeff/np.tanh(0.5*beta*omega_p))
gl_pole = - basis_b.s * rhol_pole

plt.semilogy(np.abs(rhol_pole), marker="o", label=r"$|\rho_l|$")
plt.semilogy(np.abs(gl_pole), marker="x", label=r"$|g_l|$")

plt.xlabel(r"$l$")
plt.ylim([1e-5, 1e+1])
plt.legend()
plt.show()

/opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/sparse_ir/basis.py:58: UserWarning: 
Requested accuracy is 1e-10, which is below the
accuracy 1e-08 for the work data type <class 'numpy.float64'>.
Expect singular values and basis functions for large l to
have lower precision than the cutoff.
Install the xprec package to gain more precision.

  sve_result = sve.compute(self._kernel, eps)

Alternatively, we can use spr (sparse pole presentation) module.

from sparse_ir.spr import SparsePoleRepresentation
sp = SparsePoleRepresentation(basis_b, omega_p)
gl_pole2 = sp.to_IR(coeff)

plt.semilogy(np.abs(gl_pole2), marker="x", label=r"$|g_l|$ from SPR")
plt.semilogy(np.abs(gl_pole), marker="x", label=r"$|g_l|$")


plt.xlabel(r"$l$")
plt.ylim([1e-5, 1e+1])
plt.legend()
plt.show()

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[2], line 1
----> 1 from sparse_ir.spr import SparsePoleRepresentation
      2 sp = SparsePoleRepresentation(basis_b, omega_p)
      3 gl_pole2 = sp.to_IR(coeff)

ModuleNotFoundError: No module named 'sparse_ir.spr'

From smooth spectral function

For a smooth spectral function \(\rho(\omega)\), the expansion coefficients can be evaluated by computing the integral

\[ \begin{align} \rho_l &= \int_{-\wmax}^\wmax \dd \omega V_l(\omega) \rho(\omega). \end{align} \]

One might consider to use the Gauss-Legendre quadrature. As seen in previous sections, the distribution of \(V_l(\omega)\) is much denser than Legendre polynomial \(P_l(x(\tau))\) around \(\tau=0, \beta\). Thus, evaluating the integral precisely requires the use of composite Gauss–Legendre quadrature, where the whole inteval \([-\wmax, \wmax]\) is divided to subintervals and the normal Gauss-Legendre quadrature is applied to each interval. The roots of \(V_l(\omega)\) for the highest \(l\) used in the expansion is a reasonable choice of the division points. If \(\rho(\omega)\) is smooth enough within each subinterval, the result converges exponentially with increasing the degree of the Gauss-Legendre quadrature.

Below, we demonstrate how to compute \(\rho_l\) for a spectral function consisting of of three Gausssian peaks using the composite Gauss-Legendre quadrature. Then, \(\rho_l\) can be transformed to \(g_l\) by multiplying it with \(- S_l\).

# Three Gaussian peaks (normalized to 1)
gaussian = lambda x, mu, sigma:\
    np.exp(-((x-mu)/sigma)**2)/(np.sqrt(np.pi)*sigma)

rho = lambda omega: 0.2*gaussian(omega, 0.0, 0.15) + \
    0.4*gaussian(omega, 1.0, 0.8) + 0.4*gaussian(omega, -1.0, 0.8)

omegas = np.linspace(-5, 5, 1000)
plt.xlabel(r"$\omega$")
plt.ylabel(r"$\rho(\omega)$")
plt.plot(omegas, rho(omegas))
plt.show()

beta = 10
wmax = 10
basis = sparse_ir.FiniteTempBasis("F", beta, wmax, eps=1e-10)

rhol = basis.v.overlap(rho)
gl = - basis.s * rhol

plt.semilogy(np.abs(rhol), marker="o", label=r"$|\rho_l|$")
plt.semilogy(np.abs(gl), marker="x", label=r"$|g_l|$")
plt.xlabel(r"$l$")
plt.ylim([1e-5, 1])
plt.legend()
plt.show()

\(\rho_l\) is evaluated on arbitrary real frequencies as follows.

rho_omgea_reconst = basis.v(omegas).T @ rhol

plt.xlabel(r"$\omega$")
plt.ylabel(r"$\rho(\omega)$")
plt.plot(omegas, rho(omegas))
plt.show()

From IR to imaginary time

We are now ready to evaluate \(g_l\) on arbitrary \(\tau\) points. A naive way is as follows.

taus = np.linspace(0, beta, 1000)
gtau1 = basis.u(taus).T @ gl
plt.plot(taus, gtau1)
plt.xlabel(r"$\tau$")
plt.ylabel(r"$G(\tau)$")
plt.show()

Alternatively, we can use TauSampling as follows.

smpl = sparse_ir.TauSampling(basis, taus)
gtau2 = smpl.evaluate(gl)
plt.plot(taus, gtau1)
plt.xlabel(r"$\tau$")
plt.ylabel(r"$G(\tau)$")
plt.show()

From full imaginary-time data

A numerically stable way to expand \(G(\tau)\) in IR is evaluating the integral

\[ G_l = \int_0^\beta \dd \tau G(\tau) U_l(\tau). \]

You can use overlap function as well.

def eval_gtau(taus):
    uval = basis.u(taus) #(nl, ntau)
    return uval.T @ gl

gl_reconst = basis.u.overlap(eval_gtau)

plt.semilogy(np.abs(gl_reconst), label="reconstructed", marker="o")
plt.semilogy(np.abs(gl), label="exact", marker="x")
plt.semilogy(np.abs(gl_reconst - gl), label="error", marker="")
plt.xlabel(r"$l$")
plt.xlabel(r"$|g_l|$")
plt.ylim([1e-20, 1])
plt.legend()
plt.show()