Intermediate representation (IR)

\[ \newcommand{\iv}{{\mathrm{i}\nu}} \newcommand{\wmax}{{\omega_\mathrm{max}}} \newcommand{\dd}{{\mathrm{d}}} \]

One-particle Green’s function

We introduce a Green’s function with imaginary arguments in time and frequency. This has no physical meaning but is merely a mathematical trick and makes calculations easier (to give another example of this: in Minsowski spacetime we take advantage of a similiar substitution)

The so-called imaginary-frequency (Matsubara) Green’s functions are defined as followed:

\[ G_{ij}(\tau-\tau') = -\langle T_\tau [c_i(\tau){c}^\dagger_j(\tau')]\rangle, \]

where \(i\) and \(j\) denote spin/orbital/band and \(T_\tau\) is the time-ordering operator. Here \(\tau\) represents a imaginary time unit \(\mathrm{i}t\), while \(c_i\)/\(c_j\) is a fermionic or bosonic annihilation/creation operator.

The Fourier Transformation of \(G_{ij}(\tau)\) (with \(\tau \in [0,\beta]\)) reads

\[ G_{ij}(\iv_n) = \int_0^{\beta} \dd \tau e^{\iv_n\tau} G_{ij}(\tau), \]

where \(\nu_n = (2n+1)\pi/\beta\) (fermion) and \(\nu_n = 2n\pi/\beta\) (boson) with \(n\) being an integer. The inverse temperature is denoted by \(\beta\) (We take \(\hbar=1\)). The inverse transformation is given by

\[ G_{ij}(\tau) = \frac{1}{\beta}\sum_{n=-\infty}^\infty e^{-\iv_n\tau}G_{ij}(\iv_n). \]

Continuing \(G_{ij}(\iv_n)\) to a holomorphic function in the upper half of the complex plane, the imaginary-frequency (Matsubara) Green’s function can be related to the “orginary” retarded Green’s function as

\[ G_{ij}^\mathrm{R}(\omega)=G_{ij}(z \rightarrow \omega+\mathrm{i}0^{+}). \]

In the following, we omit the symbols \(i\), \(j\), \(n\) unless there is confusion.

Lehmann representation

In the imaginary-frequency domain, the Lehmann representation reads

\[ \begin{align} G(\iv) &= \int_{-\infty}^\infty \dd\omega \underbrace{\frac{1}{\iv - \omega}}_{\equiv K(\iv, \omega)} A(\omega), \end{align} \]

where \(A(\omega)\) is a spectral function. \(K(\iv, \omega)\) is the so-called analytic continuation kernel. The Lehmann representation can be transformed to the imaginary-time domain as

(1)\[ \begin{align} G(\tau) &= - \int_{-\infty}^\infty \dd\omega K(\tau, \omega) A(\omega), \end{align} \]

where \(0 < \tau < \beta\) and

\[\begin{split} \begin{align} K(\tau, \omega) &\equiv - \frac{1}{\beta} \sum_{\iv} e^{-\iv \tau} K(\iv, \omega) = \begin{cases} \frac{e^{-\tau\omega}}{1+e^{-\beta\omega}} & (\mathrm{fermion}),\\ \frac{e^{-\tau\omega}}{1-e^{-\beta\omega}} & (\mathrm{boson}) \end{cases}. \end{align} \end{split}\]

The minus sign originates from our the convention \(K(\tau, \omega) > 0\). To avoid the divergence of the bosonic kernel at \(\omega=0\), we reformulate Eq. (1) as

\[ \begin{equation} G(\tau)= - \int_{-\infty}^\infty\dd{\omega} K^\mathrm{L}(\tau,\omega) \rho(\omega), \end{equation} \]

where \(K^\mathrm{L}(\tau, \omega)\) is the “logistic kernel” defined as

(2)\[ K^\mathrm{L}(\tau, \omega) = \frac{e^{-\tau\omega}}{1+e^{-\beta\omega}}, \]

and \(\rho(\omega)\) is the modified spectral function

\[\begin{split} \begin{align} \rho(\omega) &\equiv \begin{cases} A(\omega) & (\mathrm{fermion}),\\ \frac{A(\omega)}{\tanh(\beta \omega/2)} & (\mathrm{boson}). \end{cases} \end{align} \end{split}\]

Singular value expansion and basis functions

The singular value expnasion of the kernel (2) reads [Shinaoka et al., 2017]

\[ K^\mathrm{L}(\tau, \omega) = \sum_{l=0}^\infty U_l(\tau) S_l V_l(\omega), \]

for \(\omega \in [-\wmax, \wmax]\) with \(\wmax\) (>0) being a cut-off frequency. \(U_l(\tau)\) and \(V_l(\omega)\) are left and right singular functions and \(S_l\) as the singular values (with \(S_0>S_1>S_2>...>0\)). The two sets of singular functions \(U\) and \(V\) make up the basis functions of the so-called Intermediate Representation (IR), which depends on \(\beta\) and the cutoff \(\wmax\). For the peculiar choice of the regularization for the bosonic kernel using \(K^\mathrm{L}\), these basis functions do not depend on statistical properties. The basis functions \(U_l(\tau)\) are transformed to the imaginary-frequency axis as

\[ U_l(\iv) \equiv \int_0^\beta \dd \omega e^{\iv \tau} U_l(\tau). \]

Some of the information regarding real-frequency properties of the system is often lost during transition into the imaginary-time domain, so that the imaginary-frequency Green’s function does hold less information than the real-frequency Green’s function. The reason for using IR lies within its compactness and ability to display that information in imaginary quantities.

The decay of the singular values depends on \(\beta\) and \(\wmax\) only through the dimensionless parameter \(\Lambda\equiv \beta\wmax\). The following plots show the singular values and the basis functions computed for \(\beta=10\) and \(\wmax=10\).

import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import sparse_ir

plt.rcParams.update({
    "font.family": "serif",
    "font.size": 16,
})

lambda_ = 100
beta = 10
wmax = lambda_/beta
basis = sparse_ir.FiniteTempBasis('F', beta, wmax, eps=1e-10)

plt.semilogy(basis.s, marker='o', ls='')
plt.xlabel(r'$l$')
plt.ylabel(r'$S_l$')
plt.tight_layout()
plt.show()

/opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/sparse_ir/basis.py:58: UserWarning: 
Requested accuracy is 1e-10, which is below the
accuracy 1e-08 for the work data type <class 'numpy.float64'>.
Expect singular values and basis functions for large l to
have lower precision than the cutoff.
Install the xprec package to gain more precision.

  sve_result = sve.compute(self._kernel, eps)

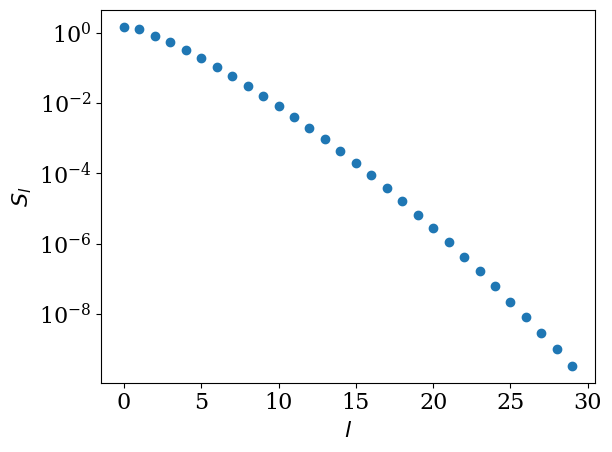
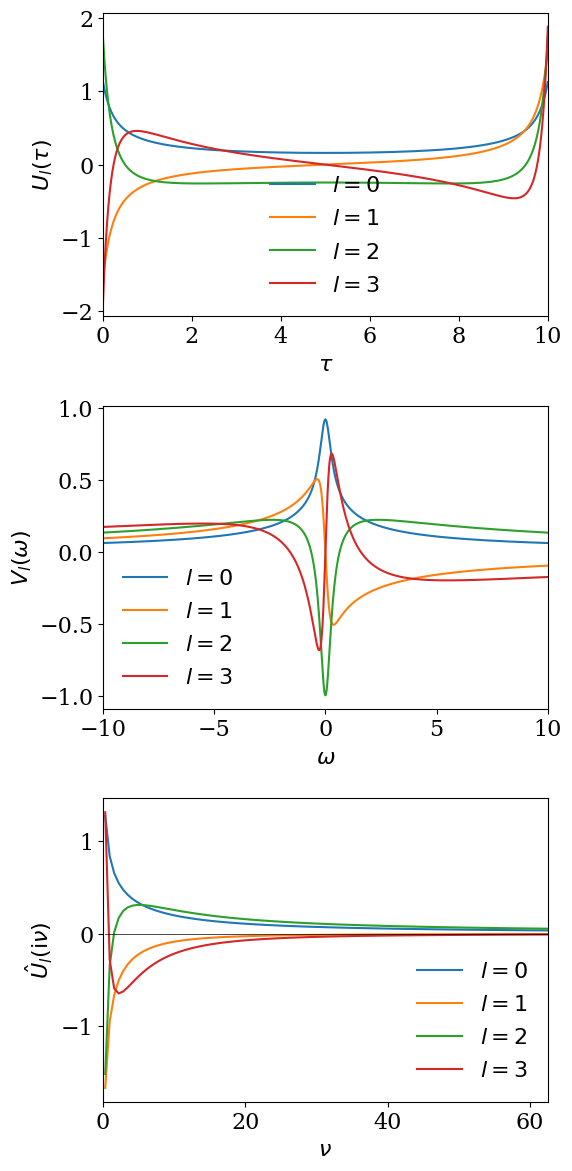
fig = plt.figure(figsize=(6,12))
ax1 = plt.subplot(311)
ax2 = plt.subplot(312)
ax3 = plt.subplot(313)
axes = [ax1, ax2, ax3]

taus = np.linspace(0, beta, 1000)
omegas = np.linspace(-wmax, wmax, 1000)

beta = 10
nmax = 100

v = 2*np.arange(nmax)+1
iv = 1J * (2*np.arange(nmax)+1) * np.pi/beta

uhat_val = basis.uhat(v)
for l in range(4):
    ax1.plot(taus, basis.u[l](taus), label=f'$l={l}$')
    ax2.plot(omegas, basis.v[l](omegas), label=f'$l={l}$')
    y = uhat_val[l,:].imag if l%2 == 0 else uhat_val[l,:].real
    ax3.plot(iv.imag, y, label=f'$l={l}$')

ax1.set_xlabel(r'$\tau$')
ax2.set_xlabel(r'$\omega$')
ax1.set_ylabel(r'$U_l(\tau)$')
ax2.set_ylabel(r'$V_l(\omega)$')
ax1.set_xlim([0,beta])
ax2.set_xlim([-wmax, wmax])

ax3.plot(iv.imag, np.zeros_like(iv.imag), ls='-', lw=0.5, color='k')
ax3.set_xlabel(r'$\nu$')
ax3.set_ylabel(r'$\hat{U}_l(\mathrm{i}\nu)$')
ax3.set_xlim([0, iv.imag.max()])

for ax in axes:
    ax.legend(loc='best', frameon=False)

plt.tight_layout()